点Pはなぜ動く…？「点P」と「関数」の意外な関係性【数学のギモン】

みんな大好き「動く点P」

突然ですが、皆さんにクイズです。

図のような1辺が6cmの正方形ABCDがあり、点Pがその辺上を毎秒1cmの速さで点Bから点Cを通って点Dまで移動します。そのとき、△DBPの面積が9cm2になるのは何秒後でしょうか？

いかがでしょう。この問題を見た瞬間に懐かしさを覚えた人も多いのではないでしょうか。

中学数学で頻出の分野であり、多くの人を困らせてきたいわゆる「動く点P」問題です。学生時代にこの「点P」に苦しめられた人も少なくないでしょう。

この問題の正攻法は、「x秒後に面積が9cm2になる」と仮定し、そのxについての式を立てて答えを求めるやり方となります。点P問題に限らず、数学の文章題ではこのように「求めるものを文字で置く」考え方は重要になります。

しかし実は、このような問題は「グラフ」を用いて視覚的にとらえることで、格段に解きやすくなるのです。

今回は、昔懐かしい点P問題の複数の解き方を解説しながら、「点Pが動く」とは何を意味しているのか、そして「関数」とはいったいどのようなものなのかについて解説していきます。

文章題を「式」で解く

さて、まずは冒頭で紹介した問題を、「x秒後」についての式を立てる方法で解いていきましょう。

この問題では、点Pは「点B」を出発し、「点C」を通って最終的に「点D」まで移動します。つまり、点Pには辺BC上を移動している時間と、辺CD上を移動している時間があることが分かります。

実際に三角形を作ってみると分かるのですが、このどちらの状態かによって三角形の位置や向きは変化します。

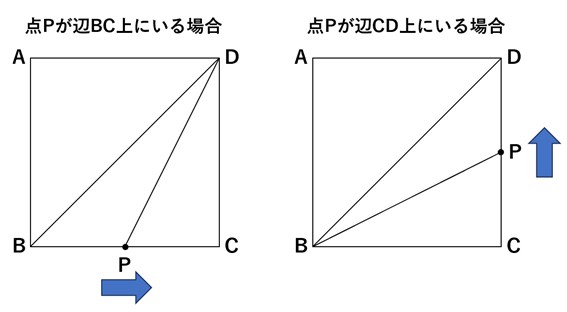
実際に三角形を作ってみると、この図のようになります。

三角形の面積は皆さんもご存知の通り「底辺×高さ÷2」で求めることができるのですが、この「高さ」は底辺に対して垂直でなければなりません。そのため、点Pが辺BC上にいる場合と辺CD上にいる場合で、「底辺」「高さ」がそれぞれどの長さになるかが変わってくるのです。

・点Pが辺BC上にいる場合

この場合、△DBPは底辺が「辺BP」、高さが「辺CD」の長さの三角形と捉えることができます。辺CDは6cmと分かっているため、辺BPの長さが何cmかが分かれば面積を求められることになります。ここで、上で示した「x秒後」の仮定を使うのです。

点Pは毎秒1cmの速さで動くため、例えば1秒後であれば点Bから1cm、3秒後であれば点Bから3cm進むことになります。つまり、x秒後の点Pの位置は、点Bからちょうどxcm進んだ場所にあることが分かります。よって、x秒後の辺BPの長さは「xcm」と置くことができます。

よって、△DBPの面積は

底辺×高さ÷2 = x(cm)×6(cm)÷2 = 3x(cm2)

と表すことができます。

ちなみに、点Pは進み続けると6秒後に点Cに到着します。それ以降は「辺BC上にいる場合」という条件を満たさなくなるため、ここで考えているxは0から6までの範囲に限定されていることになります。

点Pを動かすと…

・点Pが辺CD上にいる場合

問題はこちらです。まず、辺CD上にいるということは、点Bを出発した点Pはすでに点Cまでは移動していることを示しています。つまり、少なくとも6秒以上時間が経過しているということです。

そのうえで、今回は底辺が「辺PD」、高さが「辺BC」の長さの三角形と捉えることができ、考えるべきは「辺PD」の長さがどう変化するかだと分かります。

これもいくつか例を挙げて考えてみましょう。

点Pの位置が点Cと重なるとき、つまり6秒後では、辺PDの長さは辺CDと同じ6cmとなります。ここから1秒進んで7秒後になると、点Pは辺D側に1cm近づくため、辺PDの長さは1cm短くなって5cmとなります。8秒後、9秒後…と時間が進むにつれて徐々に辺PDの長さは短くなり、12秒後に点Pが点Dと到着します。

つまり、経った秒数と辺PDの長さの関係性は、表で表すと次のようになります。

これを見ると、xが大きくなるとそれと同じペースで辺PDの長さは短くなり、どの列も上下の数字を足すと12になることが分かります。よって、x秒後の辺PDの長さは「12-x(cm)」と表すことができます。よって、この場合の△DBPの面積は

底辺×高さ÷2 = (12-x)(cm)×6(cm)÷2 = 3(12-x) (cm2)

と表すことができます。

・面積を「x」で表す

この2つをまとめると、△DBPの面積は

xが0から6までの数字のとき→3x(cm2)

xが6から12までの数字のとき→3(12-x) (cm2)

であると分かります。あとは、面積がちょうど9cm2になるxを求めれば良いため、

3x=9

を解いてx=3（このxは0から6までの条件を満たす）、そして

3(12-x)=9

を解いてx=9（このxは6から12までの条件を満たす）となり、答えは「3秒後と9秒後」と求まるのです。

いかがでしたでしょうか。もちろん丁寧に説明しすぎた部分もありますが、正直、「やっぱりめんどくさいな」と思った人が多いのではないでしょうか。

そう思った人には、これから説明する「グラフ」の考え方をオススメします。

グラフで考える

先ほどの点Pの動きを、時間経過を横軸で、そして面積を縦軸で表してみましょう。

点Pは点Bを出発し、点Cに到着するまでは、面積は一定のペースで増えていきます。そして、6秒後に点Cに到着したときに最大となり、そのとき△DBPは底辺も高さも6cmとなるため、面積は

底辺×高さ÷2 = 6(cm)×6(cm)÷2 = 18(cm2)

となります。

点Cを通過すると、点Dに向けて点Pが動いていきます。先ほども確認した通り、どんどんと三角形は小さくなり、12秒後に面積は0になる（三角形が消滅する）ことが分かります。

この動きをグラフで表すと、次のようになります。

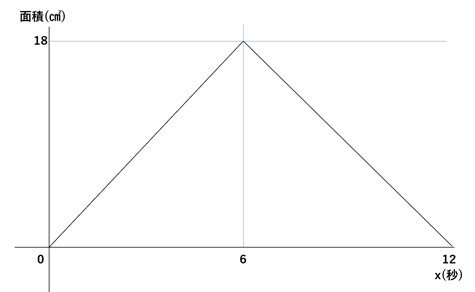
このようにグラフで示すと、点Pが動くにつれて面積が徐々に大きくなり、点Cを通過したタイミングで逆に面積が小さくなっていくことが視覚的に分かります。

そして、ここに面積9cm2のラインで1本の横線を引くと、このようになります。

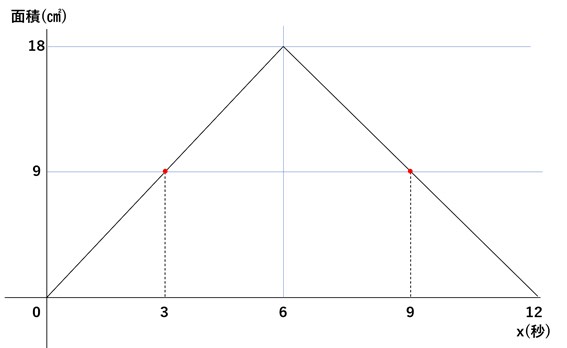
面積9cm2はちょうど18cm2の半分となるため、最初に到達するのは6秒後の半分で3秒後、そして2度目に重なるのは9秒後であることが一目で見て分かります。このようにグラフで考えると、複数の式を解く必要がなく問題に答えを出すことができるのです。

「関数」は数学の世界だけではない

いかがでしたでしょうか。「動く点P問題」を面倒で複雑な計算ばかりだと思っていた方も、グラフを用いると見え方が少し変わったのではないでしょうか。

点Pが出発してからの「時間」が変化するのにともなって、「面積」も変化していく。このような「ともなって変わる数」のことを「関わる（かかわる）」という言葉を用いて「関数」と呼びます。

この「関数」の考え方は、数学の勉強だけに限らず、ビジネスや日常生活の中にも頻繁に登場しています。

たとえば営業職で「広告費を増やしたら、どのくらい売上が伸びるか」を考えるとき。

これはまさに、「入力（広告費）」と「出力（売上）」の関係を読み解く関数の世界です。

当たり前ですが、「費用を2倍にしたら売上も2倍になる」とは限りません。

途中で伸びが鈍化したり、頭打ちになったり、はたまた圧倒的な効果を生み出したり。

その動きを把握するためにも、「関数」の理解は非常に重要になります。

点Pとは、数学の世界で“変化するもの”の象徴として用いられています。

日常生活でも仕事でも、変化するものはたくさんあります。

顧客のニーズ、アクセス数、モチベーション、株価…

どれも時間や条件によって動く“点P”のような存在です。

かつて習った「動く点Pの問題」への考え方が、日常のちょっとした悩みやビジネスでの課題を解決するヒントになるかもしれません。